Ord og begreper
Eksempler:
regneart, gjentatt addisjon, multiplikasjon, multiplisere, gange, gangetegn/multiplikasjonstegn, grupper, den lille multiplikasjonstabellen/gangetabellen, pugge/automatisere
faktorer: tallene som multipliseres med hverandre
produkt: resultatet av en multiplikasjon
Litt om å undervise i multiplikasjon
Multiplikasjon er en regneart som må forstås, og multiplikasjonstabellen må automatiseres. Den har trenger vi til både hoderegning og oppgaveløsning. Det viktigste er å forstå hva begrepet multiplikasjon innebærer. Bli trygg på regnestrategiene og legg vekt på at et multiplikasjonsstykke kan løses på flere ulike måter.
La elevene være detektiver og selv få utforske tallmønstre og sammenhenger mellom tallene. Gi ledetråder og veiledning underveis.
Vis hvor viktig det er å kunne bruke tegning som regneverktøy, og at tegning er til god hjelp dersom vi ikke er sikre på svaret.
I undervisningen er det er viktig å variere mellom alle de ulike uttrykksmåtene slik at elevene gjøres kjent med at regnestykket kan leses på flere måter. 3 x 4 kan leses som:
– 3 multiplisert med 4
– 3 ganger med 4
– 3 grupper med 4
– 3 eksemplar av 4
– 3 av 4
– 3 firere
Slik klassifiserer vi multiplikative strukturer:
– Like grupper
– Rutenett (areal)
– Forstørring
– Forhold mellom tall
– Sammenligning
Den lille gangetabellen, oversikt
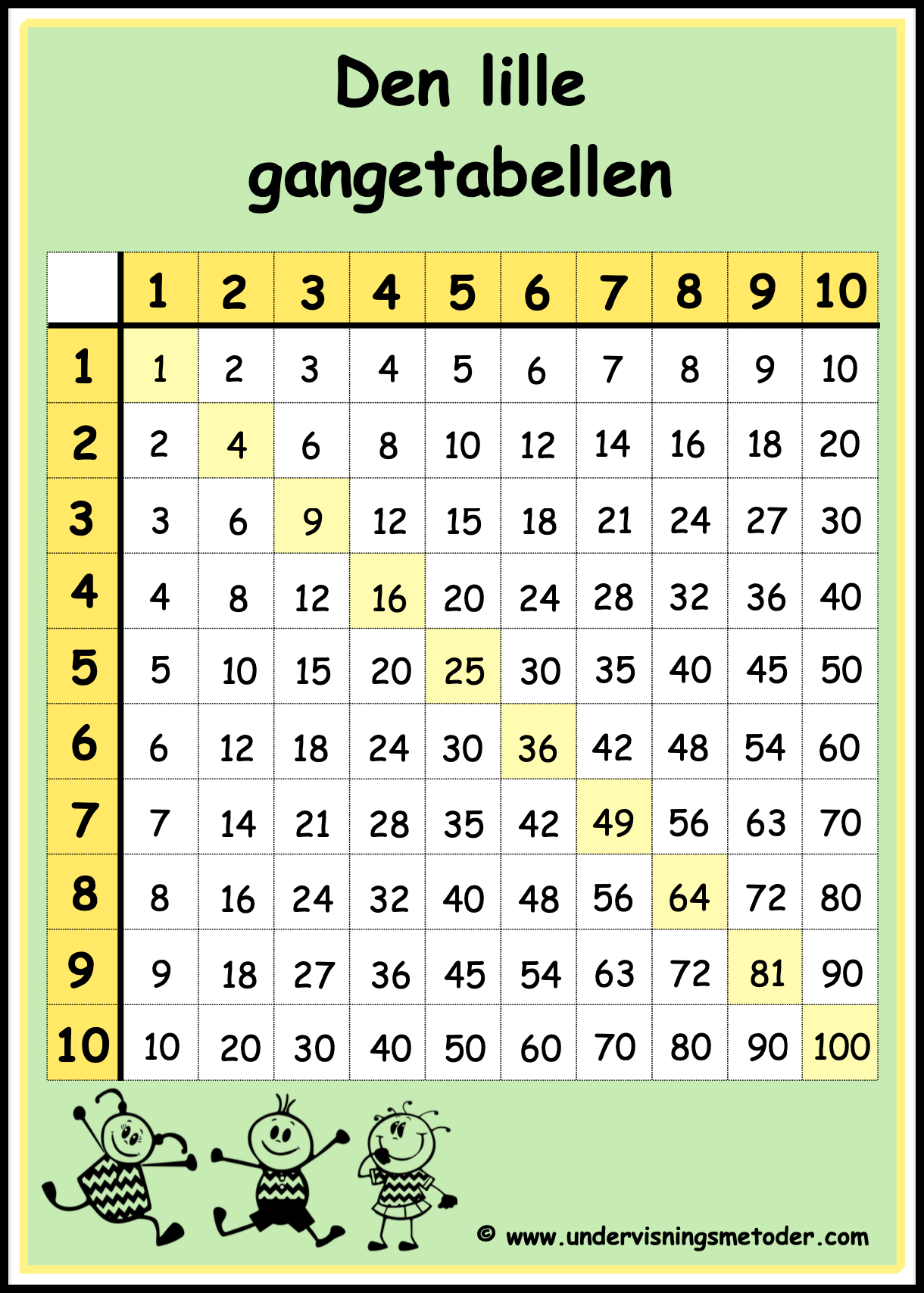
Innføring
NRK super
MK-X – ganging
(15 min)
Rekketelling
– Tell med to og to, tre og tre, fire og fire, avhengig av hvilken gangetabell dere skal lære.
– Last ned gratis arbeidsark på www.multiplication.com.
Oppgavehefter


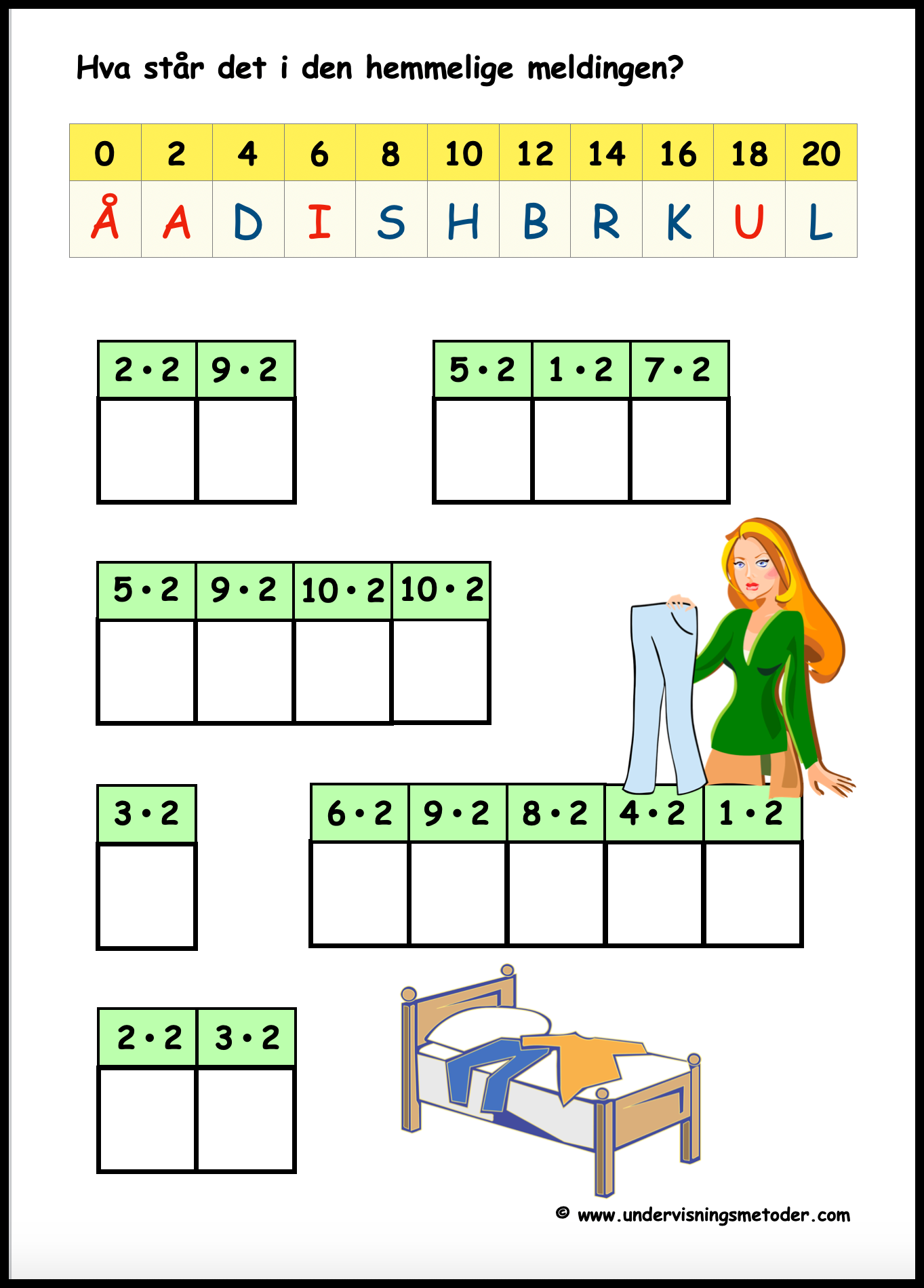
BOKMÅL
NYNORSK

Viklekort, 10 viklekort – et til hver tabell

Skriv ut viklekortene. Om du ønsker kan du lage et riss på baksiden som viser fasiten, slik at elevene kan sjekke om de har gjort det riktig på egen hånd (men dette er ikke nødvendig). Et alternativ er å ha en oversikt med gangetabellene liggende ved siden av.
Laminer alle kortene og lag et hull med hullemaskin øverst, hvor du fester tråden.
Viklekort kan brukes både inne og på uteskole.
Viklekort er fint å bruke som stasjonsaktivitet, men også som ekstraarbeid. Selv har jeg også god erfaring med å bruke viklekort som avbrekk for elever som strever med å skrive. For disse elevene kan slike aktiviteter være et kjærkomment avbrekk fra skriftlige oppgaver.
Viklekortene finner du HER i nettbutikken!
Bingo
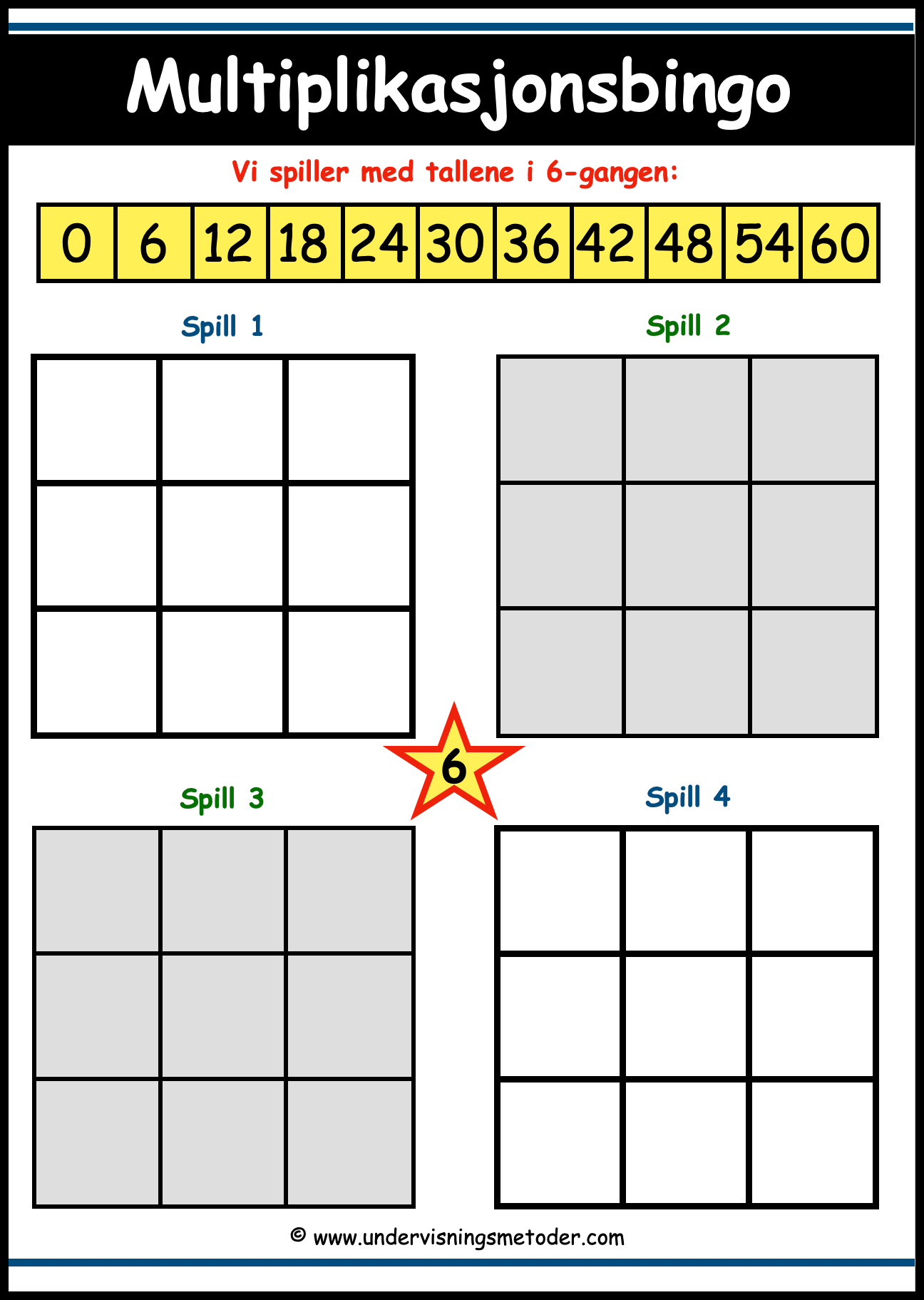
Denne multiplikasjonsbingoen kan fint inngå som en sisteside i oppgaveheftene overfor.
Fyll inn tall fra multiplikasjonstabellen dere jobber med på bingospillene.
Læreren skriver opp et multiplikasjonsstykke på tavla (f.eks: 4 x 3 =), og de elevene som har 12 på bingobrettet sitt får sette et kryss på tallet.
Eleven som først har tre kryss på rad vannrett, loddrett eller på skrå, roper så «BINGO!». Deretter må eleven fortelle hvilke tall på bingobrettet sitt som er krysset av.
BOKMÅL
NYNORSK
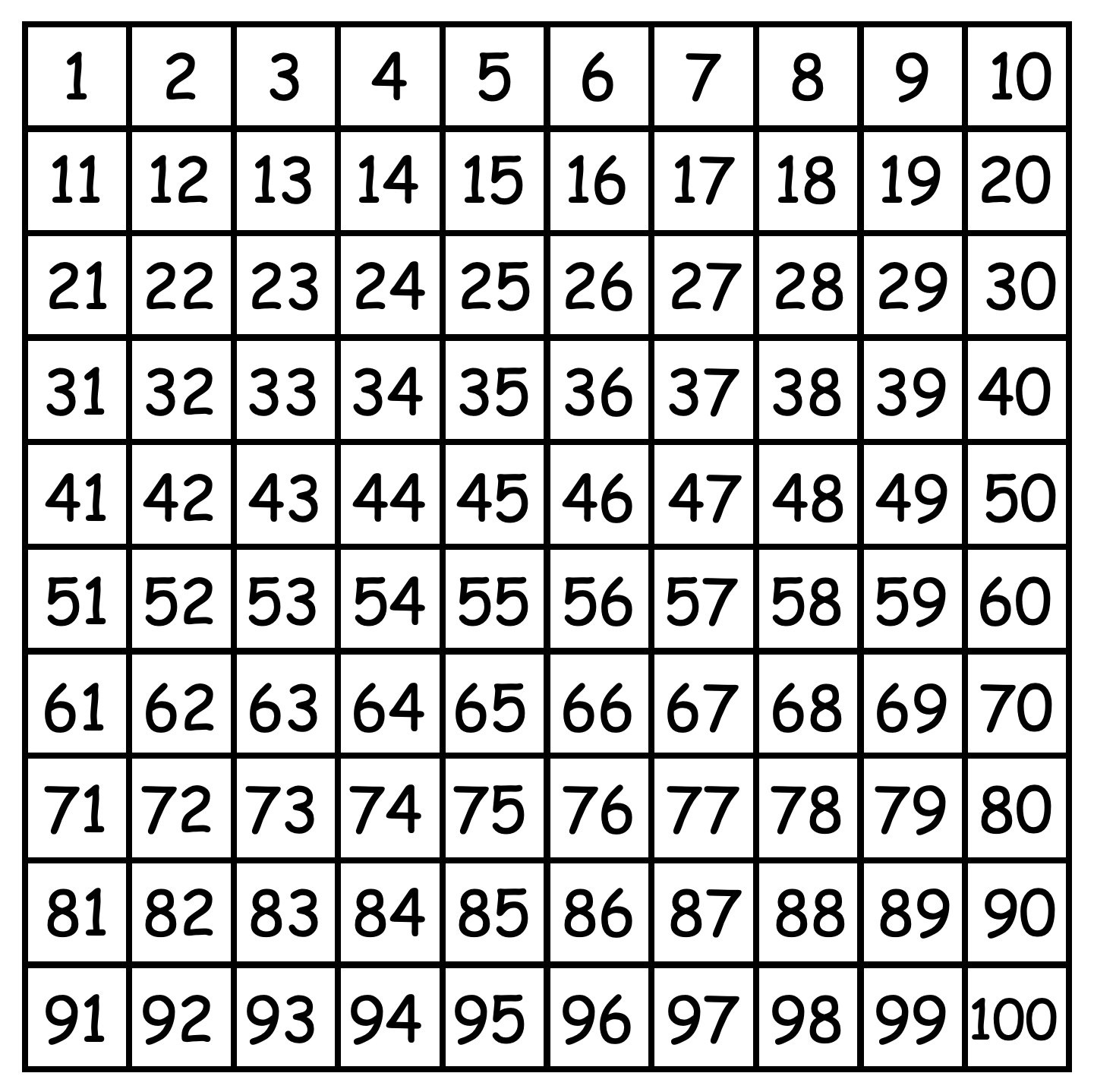
Hundrernett til felles gjennomgang på smartboard
Her er det et hundrernett du kan bruke til felles gjennomgang. Slå det opp stort på smartboarden og marker rutene i den aktuelle gangetabellen dere undersøker. Hvilke mønstre og sammenhenger finner dere?
Gangetriks
0-gangen
Dersom du multipliserer et tall med 0, vil svaret alltid bli 0.
1-gangen
Dersom du multipliserer et tall med 1, vil du alltid få samme tall.
2-gangen
Dersom du multipliserer et tall med 2, er trikset dobling! Alle tall i 2-gangen er partall.
3-gangen
Dersom du multipliserer et tall med 3, vil tverrsummen av sifrene i svaret alltid være 3, 6 eller 9.
4-gangen
Dersom du multipliserer et tall med 4, kan du finne svaret ved å ta det dobbelte av det dobbelte. Tallene i 4-gangen er altså det dobbelte av tallene i 2-gangen. Derfor må også tallene i 4-gangen være partall. Et mønster i 4-gangen er at tallene slutter på 4, 8, 2, 6, 0, osv, om og om igjen.
5-gangen
Dersom du multipliserer et tall med 5, kan du finne svaret ved å halvere tallene i 10-gangen. Et mønster er at alle tallene i 5-gangen slutter på 5 eller 0.
Hvis du multipliserer 5 med et partall, vil svaret (nesten) alltid slutte på 0.
Hvis du multipliserer 5 med et oddetall, vil svaret alltid slutte på 5.
5-gangen hjelper deg å se hva klokka er. Det er 5 min mellom hvert tall på urskiven.
6-gangen
Dersom du multipliserer et tall med 6, kan du finne svaret ved først multiplisere tallet med 5, for deretter å legge til en gruppe.
Når du multipliserer 6 med et partall, vil svaret slutte på det samme tallet du multipliserer med. I fire av multiplikasjonsstykkene i 6-gangen er det første sifferet halvparten av de andre.
7-gangen
8-gangen
Dersom du multipliserer et tall med 8, kan du multiplisere tallet med 10, for deretter å trekke fra to grupper. Siden tallene i 8-gangen er det dobbelte av tallene i 4-gangen, kan du også velge å først multiplisere tallet med 4, for deretter å doble tallet. For eksempel!
9-gangen
Dersom du multipliserer et tall med 9 er det flere gangetriks som kan hjelpe deg!
* Du kan velge å multiplisere tallet med 10, for så å trekke fra en gruppe.
* Tverrsummen vil alltid bli 9.
* I 9-gangen finner vi flere tvillingtall (09/90 – 18/81 – 27/72 – 36/63).
* I hundrerruta kan du se at sifrene på enerplassen teller ned fra 9 til 0. Fra 2×9 til 10×9 teller tierplassen opp fra 9 til 1.
*Fingertrikset: Hold hendene opp foran deg. Lillefingeren på venstre hånd er 1, lillefingeren på høyre hånd er 10. Eks: 9×5=
Ta ned den femte fingeren (tommelen på venstre hånd). Da får du fire fingre igjen til venstre for fingeren du tok ned. Dette er tierne i svaret.
Til høyre for fingeren du tok ned er det 5 fingre. Dette er enerne i svaret.
Svaret på. multiplikaszonsstykket blir derfor 45.
* Tiervenntrikset: En elev jeg hadde oppdaget enda en sammenheng. Dersom du multipliserer et tall med 10, vil sifferet på tierplassen i svaret være en mindre enn faktoren du multipliserer med 9. Videre vil sifferet på enerplassen være tiervennen til faktoren du multipliserer med 9.
Eks: 3×9 = 27 (2 fordi en mindre enn 3, 7 fordi 7 er tiervennen til 3).
* Subtraksjonstriks: Sifferet på tierplassen i svaret vil alltid være en mindre enn det tallet du skal multiplisere med 9. Sifferet på enerplass i svaret er 9 minus det første sifferet.
10-gangen
Dersom du multipliserer et tall med 10, legger du til en 0.
Dobling og halvering
Noen ganger kan det hjelpe å doble den ene faktoren og halvere den andre. Da vil svaret på multiplikasjonsstykket fortsatt bli det samme, fordi vi beholder det samme forholdet mellom faktorene. Eks:
4 x 6 =
(4 x 2) x (6 : 2) =
8 x 3 =
24
Fingertriks: Hvor mange flere enn 5?
Bøy ned like mange fingre.
(kan brukes på 5-9 – gangen)
Eks: 8 x 7 =
– Hold hendene i været med fingrene opp.
– Hvor mange flere enn 5 er den første faktoren? Bøy like mange fingre.
8 er 3 mer enn 5. Derfor bøyer vi ned 3 fingre på venstre hånd.
– Hvor mange flere enn 5 er den andre faktoren? Bøy like mange fingre.
7 er 2 mer enn 5. Derfor bøyer vi ned to fingre på høyre hånd.
– Fingrene som er nede står for tiere. Produktet av fingrene som er oppe står for enere.
I dette eksempelet er 5 fingre nede og (2×3) fingre oppe. Svaret på multiplikasjonsstykket blir derfor 56.
Uteskole
Lag gangestykker med naturmaterialer
Gå på tur i skogen, eller en annen fin plass der det er god tilgang på ulike naturmaterialer. La elevene sammen med læringspartner. Hvert par får komme frem til læreren for å trekke et kort med et multiplikasjonsstykke. Deretter skal de bruke naturmaterialer til å finne løsningen på multiplikasjonsstykket. For eksempel kan 3X5 være tre grupper med 5 kongler i hver gruppe. Læreren går rundt og tar bilder av «løsningene».
Tilbake i klasserommet viser læreren et og et bilde på smartboard. Bildet er av «løsningene» som elevene har laget av naturmaterialer, og nå skal elevene gjette hvilket regnestykke det var laget til. Læringspartnerne som har laget det som vises på bildet forteller om svaret er riktig eller galt, og hvordan de tenkte underveis.
Lag gangestykker med kritt i skolegården
Noen ganger kan det være like stas å gjøre matteoppgaver ute som inne! La elevene løse multiplikasjonsstykker med kritt ute i skolegården. Her er det mange muligheter!
- Jobb sammen to og to læringspartnere. Hvert av læringsparene går litt unna hverandre og skriver en liste med 5 multiplikasjonsstykker, men uten svaret. Når begge læringsparene er ferdige bytter man og skriver svaret på regnestykkene.
- Skriv multiplikasjonsstykker og tegn hvordan dere tenker for å finne svaret! Læreren kan gjerne ta bilder underveis til felles gjennomgang inne i klasserommet mot slutten av økta.
- To go to læringspar jobber sammen. La hvert læringsparr trekke en lapp med et multiplikasjonsstykke som de tegner løsningen på. Deretter skal de gjette hvilket multiplikasjonsstykke det andre paret har trukket, bare ved å se på tegningen.
Stiv heks med gangestykker
En elev «har den», hvis det er mange elever kan det være flere. Den (eller de) som «har den» skal fryse de andre ved å ta på de og si «Stiv heks!». De som blir tatt blir «stiv heks» og må stille seg i frysposisjon med beina fra hverandre og armene ut til sidene. De deltakerne som ikke blir tatt kan befri de andre ved å si et multiplikasjonsstykke, og hvis de får riktig svar, kryper de gjennom beina, og vedkommende er befridd. En viktig regel er også at det ikke er lov til å ta noen som holder på å befri noen andre.
Rutenett ute i skolegården
Tegn opp 3×3 ruter ute i skolegården. Skriv svarene fra en av gangetabellene i rutene hulter til bulter. Elevene konkurrerer om å hoppe fortest fra rute til rute, samtidig som de sier tallrekkene. La en elev på hver gruppe ta tiden.
Erteposer
La elevene stå enten i en ring, eller på rekke. Si et multiplikasjonsstykke og kast erteposen til en av elevene som skal si svaret (med eller uten hjelp fra de andre), for så å kaste erteposen tilbake.
Gangeballen
Skriv et tall fra 0-10 i hver av rutene på en fotball. Det er lurt å skrive med tusj.
«Gangeballen» går ut på at elevene står i ring og kaster ballen til hverandre. Når de får ballen må de ta den imot med to hender. Før de kaster ballen videre, må de multiplisere tallene som tomlene står på. Dette er en fin aktivitet til uteskole, men den kan også gjennomføres inne i klasserommet.
Gangestafett
Skriv lapper med multiplikasjonsstykker (men uten svaret), like mange til hvert lag. Slik kan du også lett nivådifferensiere, for alle lagene trenger ikke nødvendigvis få de samme multiplikasjonsstykkene.
La en og en fra hvert lag løpe frem og hente en lapp, for så å ta den med tilbake. Skriv så svaret på gangestykket. Det er lurt om hvert lag har noe å oppbevare det i, for eksempel en boks eller lignende.
Når alle er ferdige retter lagene hverandres oppgaver. Vinneren er laget med flest riktige multiplikasjonsoppgaver.
Puslespill
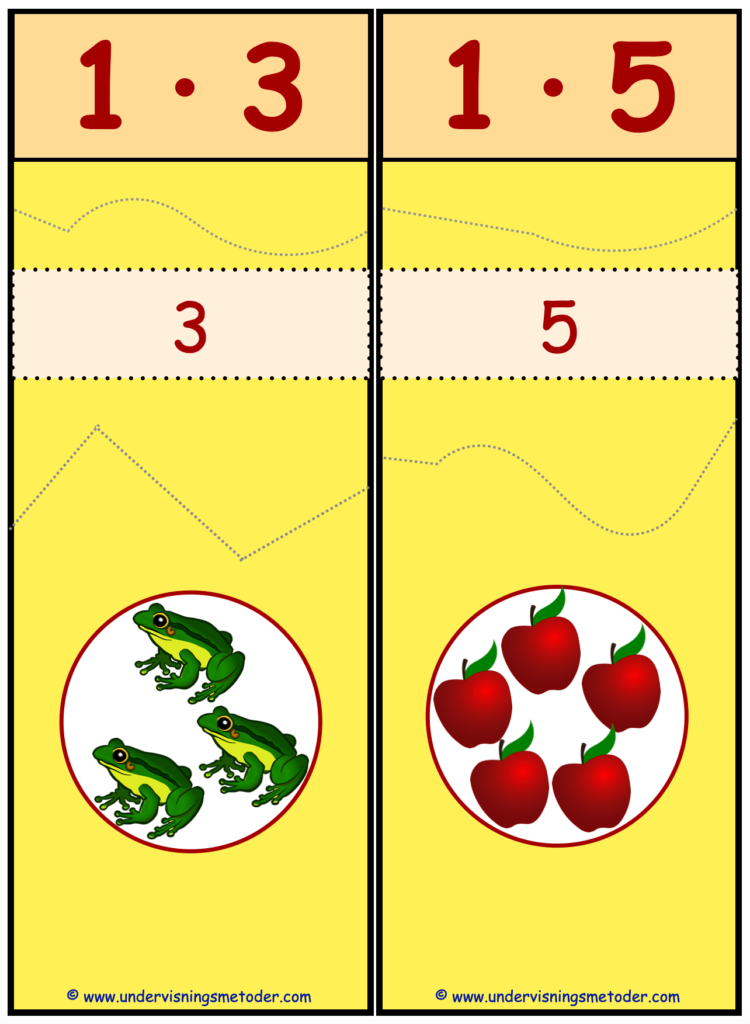
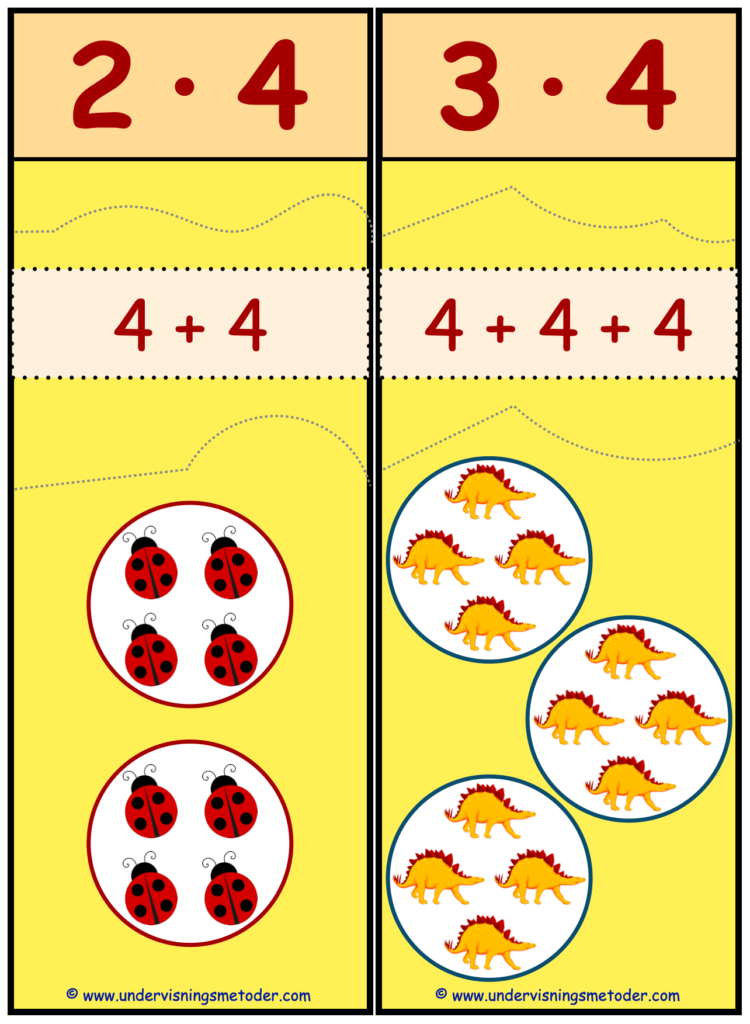
Et supert puslespill for elever som skal lære seg multiplikasjon! Dette puslespillet er et gulvpuslespill, selv om du selvfølgelig kan bruke det på pulten også. Her er det store bilder, og det er fordi dette puslespillet skal brukes til å lære elevene prinsippet i multiplikasjon: multiplikasjon er gjentatt addisjon!
Til hvert multiplikasjonsstykke er det tre brikker. En brikke der elevene forøve seg på å lese multiplikasjonsstykket, en brikke med multiplikasjonsstykket skrevet som gjentatt addisjon og en tredje brikke der multiplikasjonsstykket er visualisert med grupper, som igjen kan kobles til gjentatt addisjon.
Og til elever som ønsker litt ekstra utfordringer: Kan du lage en regnefortelling til hvert multiplikasjonsstykke?
Print ut, laminer og klipp ut puslespillbrikkene. Pass på at du følger de grå stiplede strekene når du klipper ut brikkene.
Klypekort, multiplikasjon
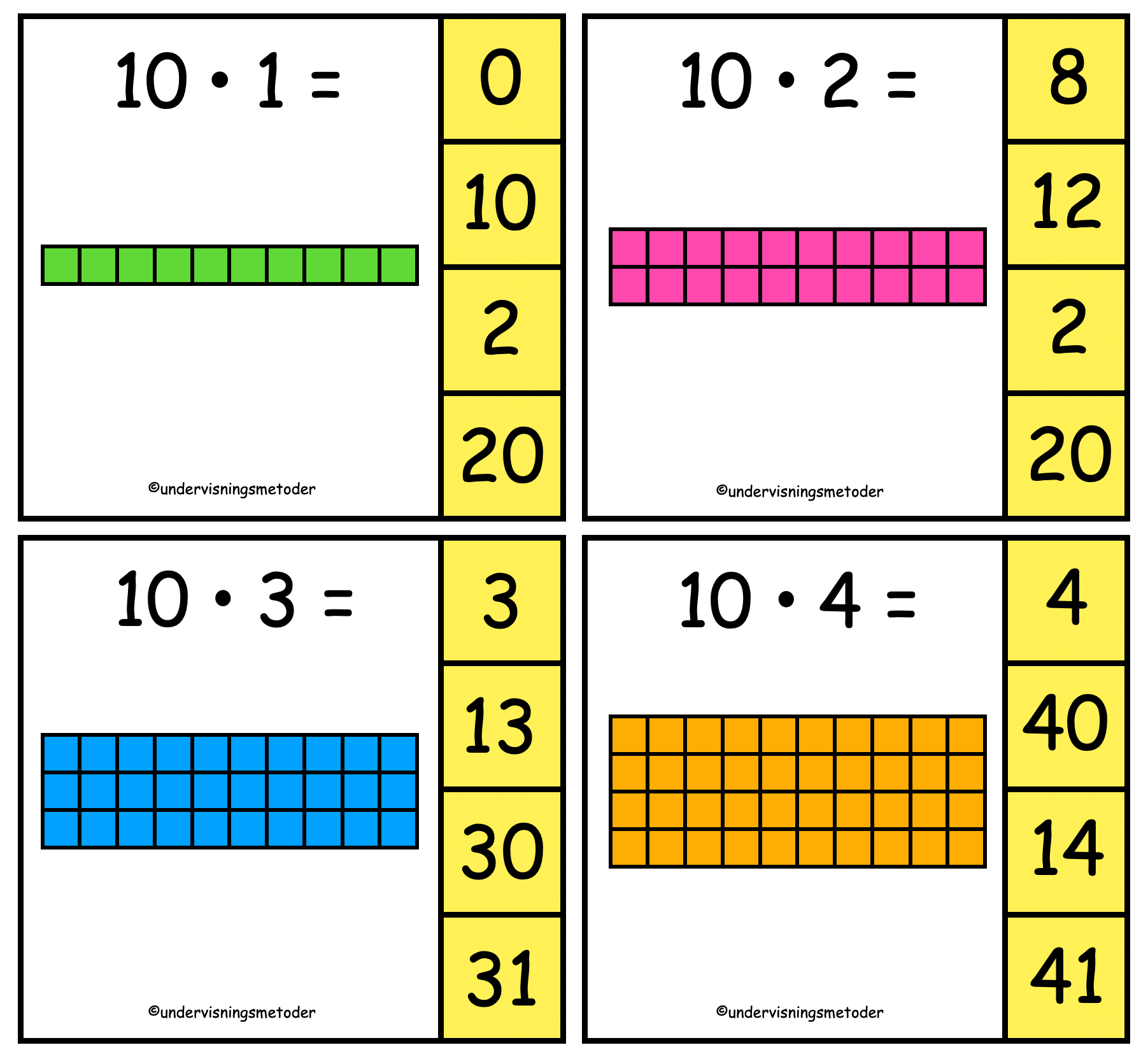
Disse klypekortene er laget for at elevene skal lære hvordan vi tenker når vi multipliserer. De kan brukes på flere ulike måter:
- Jobb sammen med læringspartner: Hver elev tar et klypekort hver, regner ut svaret og fester klesklypen på riktig svar. Deretter bytter de kort, for å sjekke om svaret er riktig.
Spør hverandre: «Hvordan tenkte du for å finne svaret?»
Skriv regnestykkene med riktig svar i skriveboka. - Diskuter på liten gruppe: Ta utgangspunkt i et klypekort, for eksempel 3 x 10. Diskuter:
Må vi skrive multiplikasjonsstykket slik, eller finnes det andre måter?
Hvordan kan vi bruke figuren på klypekortet til å vise at 10 x 3 det samme som 3 x 10?
Multiplikasjon er kommutativ, det vil si at faktorenes orden er likegyldig.
Gjelder det samme for addisjon? Hvorfor/Hvorfor ikke?
Gjelder det samme for subtraksjon? Hvorfor/Hvorfor ikke?
Jobb sammen med læringspartner. Sett klesklypen på riktig svar. Bruk skriveboka og skriv multiplikasjonsstykket på to ulike måter. - Elimineringsmetoden: Be eleven forklare (f.eks på 10 x 1) hvilke svaralternativer som ikke kan være svaret, og hvorfor. Hvorfor kan ikke svaralternativet «0» være riktig? Jo, fordi vi vet at for at svaret på et multiplikasjonsstykke skal bli 0, må den ene faktoren være 0, og det er ikke tilfellet her.

Andre leker og aktiviteter
Geobrett
Løs multiplikasjonsstykker på geobrett!
Memory
Lag gangememory med svar og regnestykker.
Finn din gangevenn
Del ut kort med gangestykke og tilsvarende kort med svar, ett til hver elev. La elevene vandre rundt i klasserommet for å finne personen som har kortet som hører til deres kort. Det er ikke tillatt å snakke. Etter hvert som de finner parr, må elevene sette seg ned i en ring og vente på at alle finner sin partner. Ta felles oppsummering der alle parrene får vist kortene sine.
Rasken
Spill sammen to og to. Hvert parr trenger en kortstokk. Ta bort knekt, dame, konge og la ess være 1. Del de resterende kortene i to, slik at hver spiller får en bunke med like mange kort. Begge spillerne snur kortene samtidig. Spilleren som først klarer å multiplisere tallene og si svaret, får stikket. Hvem får flest stikk?
Gangekrig
Ta bort bildekortene i kortstokken og del kortstokken i to, der det er like mange i hver bunke. La to elever spille mot hverandre. Spillerne legger bunken sin med kortene vendt ned. Begge spillerne snur så det første kortet. Spilleren som har kortet med høyest verdi ganger sammen tallene som kortene viser. Dersom spilleren tar feil eller ikke vet svaret, får den andre spilleren muligheten. Når man svarer riktig får man kortene. Slik fortsetter det. Vinneren er den spilleren som står igjen med flest kort.
En annen versjon er at det er førstemann til å finne svaret på gangestykket, og denne spilleren får kortene. Denne versjonen passer spesielt til de som begynner å kunne gangetabellen godt, og som skal lære seg å automatisere gangetabellen.
Gi meg ti!
Spill to og to sammen. Hver spiller må tenke på et tall mellom 0 og 10. Begge spillerne holder opp hendene og roper: «Klar, ferdig, gå!», og hold opp antallet fingre som spilleren tenker på. Hver spiller skal nå finne svaret ved å telle antall fingre på sine egne hender og multiplisere det med antall fingre motspilleren holder opp. Den som først roper ut det riktige svaret, får et poeng. Fortsett slik til en av spillerne har ti poeng.
Melkekorker
Skriv tallene fra 0 til 10 på melkekorker. Du trenger to korker med hvert tall. La elevene jobbe sammen i parr og trekke to og to korker hver. Hva blir multiplikasjonsstykket?
Maren
Sitte på pulten, si Maren istedenfor tallet.
Kortstokk
La to og to elever dele en kortstokk. Trekk et kort hver samtidig. Hvem kan regne ut gangestykket først? Bruk gjerne en tredje elev som dommer med kalkulator.
Konkurranse
Alle elevene står på stolen. To elever får konkurrere mot hverandre i å løse et regnestykke. Den som vinner blir stående, den andre setter seg. Til slutt står en vinner igjen. Husk så langt det er mulig, at to på omtrent samme nivå konkurrerer mot hverandre.
Klesklype
Skriv tall fra gangetabellene på begge sider av et A4-ark. La elevene få sette klesklypene på svar fra en gangetabell. Marker på baksiden hvilke tall som er riktige, slik at elevene har muligheten til å sjekke om svarene er riktige.
Mattestafett
Bruk f.eks. en trapp. Klassen deles i grupper. Oppgaver på toppen, løpe opp trekke en, huske oppgaven, løp til gruppen, finn rett svar sammen, oppgi svar, feil svar må samme elev hente ny oppgave, rett svar, ny elev henter oppgave. Rett svar kan gi en bokstav som til slutt blir et ord de må pusle sammen eller lignende.
Stå på pultene
La alle elevene stå på pultene. Læreren peker på en og en elev som skal telle fra 1 og oppover. For hver gang de havner på for eksempel et tall i 3-gangen, må de si et annet ord eller klappe. Dersom de bruker for lang tid eller svarer feil, må de sette seg.
Kaboom!
Skriv enten multiplikasjon på ispinner. Plasser pinnene i en dorull trekt med stoff ( eller annen smal container)Innimellom regnestykkene er det pinner hvor det står f.eks- Ta pinne fra en venn – gi bort pinne – stå over – eller ZAP ! Som betyr at alle pinnene skal tilbake i boksen. 4-5 elever på hver gruppe.
Fluesmekke
Skriv noen svar på tavla. Elevene bruker fluesmekke og slår på riktig svar.
Plakat
La elevene få lage sin egen plakat med gangetabellen dere jobber med! Dekorer plakaten med å lage tegninger til multiplikasjonsstykkene og vis ulike regnestrategier man kan bruke for å finne svaret. Ta med plakaten hjem og heng den på veggen!
Oppgaver på internett
Gangetabellen.net: Øv på gangetabellene
«På gangetabellen.net kan du øve på alle gangetabellene. Matteoppgavene er enkle og greie, slik at du kan komme i gang med å øve på gangetabellene med en gang. Velg gangetabellen du vil øve på fra listen nedenfor. Vis hva du kan i hastighetstesten eller last ned våre flotte oppgaveark.»
Matematikk.org: Regneregn
«Hvor rask er du til å regne? Du bestemmer selv hva slags regnestykker du skal få og hastigheten. For hastigheter ingen og middels får du se et treningsbevis, mens den raske hastigheten kan gi deg et diplom.» Laget for 5.-7. trinn.
Matematikk.org: Gangetesteren
«Velg én eller flere ganger og vis at du er en ekte Gangemester! Spillet har tre hastigher: ingen, middels og rask. Velger du hastigheteringen og middels, får du se et treningsbevis. Diplom får du når du klarer den raske.»
Multi: Multiplikasjon – velg gangetabell
Velg gangetabellen du vil øve på og skyt på riktig gangestykke!
Multi: Nettoppgaver – multiplikasjon
På Multi sin nettressurs finner du oppgaver for å drille multiplikasjon, men også oppgaver for å øve på sammenhengen mellom multiplikasjon og divisjon.
Gruble.net: Ganging
«Test dine multiplikasjonsferdigheter med disse spillene, både med og uten tidspress. Du kan også få utstedt gangesertifikat!»
Mathsisfun.com: Multiplication
På denne siden finner du drilleoppgaver i multiplikasjon. Egner seg best for de som er på vei til å kunne gangetabellen forholdsvis godt. Du kan velge å gjøre utfordringen på tid, eller uten tidtakelse.
Sanger
Melodi: Lisa gikk til skolen2,4,6 og 8
10, 12,14,16
18 også 20.
Få det inn i huet.
Melodi: Blåmann, blåmann
3 og 6 og 9 og 12
15, 18 og 21
24, 27
også 30, det husker du.
Mel: Nei, nei gutt
5, 10, 15,
20, 25.
30, 35 og 40.
45 og så til 50.
glemte du deg rent,
du var ikke trent
Mel: Pål sine høner
4, 8, 12 de er lette og huske,
16 og 20 de henger seg på.
24, 28 det går ei å fuske,
32, 36, også 40 må stå.
gangetabellen ja den må vi huske.
De som skal lære de må ikke fuske.
Dette er moro, ja dette må prøves,
om du rett dyktig i regning skal bli.
Melodi: Lille Petter Edderkopp
6 x 6 er trettiseks – en trollmann og ei heks
6 x 7 er førtito – nå kjører begge to
6 x 8 er førtiåtte – nå kommer de til slottet
6 x 9 er femtifire – nå må heksa gire…
Melodi: Gubba Noa
8, 16, 24, 32 og 40
48, 56, 64, 72
Det var 80, råtti,påtti,
syng den en gang til!
Youtube: Gangetabellene 6-9
Youtube: Vi ganger med sanger – den lille gangetabellen
Multiplikasjon med tosifrede tall


