I dagens blogginnlegg deler jeg et undervisningsopplegg laget for uteskole; enten om det er en matteøkt ute i skolegården eller en dagstur. Temaet er halvering/dobling og oddetall/partall – og dermed ble det også to nye temasider (!!). Her er det mye nytt undervisningsmateriell å boltre seg i.
Siden dette undervisningsopplegget blant annet innebærer at elevene tegner med kritt, er det lurt å dra til et sted med god boltringsplass på asfalt. Det bør også være naturmaterialer tilgjengelig like ved, slik at elevene kan finne f.eks. blader/pinner/strå/kongler/gress som de kan bruke i arbeidet. Selv valgte vi å legge uteskolen denne dagen til Sofienbergparken. Der er det en stor, åpen, asfaltert plass omgitt av grønne parkområder – helt perfekt for å gjennomføre dette opplegget.
Halvering, oddetall/partall – et undervisningsopplegg
DEL 1: OPPSTART
Samling – felles gjennomgang
Før avgang startet vi opp med en felles gjennomgang av tema inne i klasserommet. Elevene mine hadde lært litt om halvering og oddetall/partall fra før (se «dagens tall», beskrevet i forrige blogginnlegg). Dobling var et begrep de kunne.
I oppstarten hadde jeg en eske med klosser. To elever i klassen skulle få halvparten av klossene hver. Hvordan kan vi tenke for å finne ut hvor mange klosser hver av elevene skal få?
Vi måtte finne ut hva som menes med en «halv». En elev fortalte at «halv» kunne være en halv time, og en annen elev fortalte at en halv kunne være halvparten av et eple. For å finne halvparten av klossene konkluderte derfor elevene med at da måtte de to elevene dele klossene likt mellom seg. Vi rappet rappen fra MKX:
«For å finne halvparten av no, så må du del det i to. For. finne halvparten av no, så må du del det i to. En her, en der, en her, en der… osv».
Deretter tok vi rappen mens de to elevene fordelte klossene imellom seg. Da de var ferdig, viste det seg at de hadde delt klossene på en måte der de ikke fikk like mange. Det stemte ikke!
Da fortalte jeg om en elev jeg hadde tidligere som fant på et lurt triks for å sikre at hun delte mengden i to like store grupper. Hun tegnet opp en strek som hun kalte «delestrek» midt på arket. For å finne halvparten fordelte hun mengden likt på hver side av delestreken (to og to på linje). Jeg klistret fast en tape på gulvet for å illustrere, la 10-tallet øverst og utfordret elevene til å fordele klossene på nytt. Slik ble det tydelig for elevene at halvparten av 10 var 5, fordi det ble 5 klosser til hver elev.
«Kunne vi tenkt på en annen måte for å finne ut dette?», spurte jeg.
En elev fortalte at hun brukte dobling for å finne halvparten:
«Jeg bare leter etter et regnestykke med dobling som blir tallet jeg skal finne halvparten av. Og siden 5+5=10, må halvparten av 10 være 5».
Elevene fant ut at 10 måtte være et partall. «Hvorfor?», spurte jeg.
«Partall er tall som kan deles på 2», fortalte en elev. Vi hadde tidligere snakket om hva som menes med «par»; vi har to av noe: sokkepar, kjærestepar, osv.
«Men betyr det altså at oddetall ikke kan deles på 2?», spurte jeg.
Skråsikkerheten ble borte, og jeg kunne se at det knaket i hodene deres.
«Jeg røper ingenting. Det må vi prøve å finne ut av på uteskole i dag!»

DEL 2: ARBEIDSARK MED OPPGAVER
Elevene jobber med læringspartner
Etter litt frilek og matpause fortsatte vi å jobbe med temaet i Sofienbergparken. Jeg hadde tallkort med tallene fra 0-20 på hånda, og nå i starten brukte jeg bare partallene.
Elevene jobbet sammen med læringspartner, og hvert par fikk utdelt et oppgavehefte, en blyant og et stort kritt. Deretter spredte elevene seg utover asfalten, og hvert læringspar tegnet opp en «delelinje» med kritt. Etterpå kom de til meg og fikk et tallkort som de tok med seg tilbake. Slik kunne jeg differensiere ved å gi kort med ekstra høye tall til elever som vokser på ekstra utfordringer, og lavere tall til elever som med fordel kan fortsette å jobbe i et lavere tallområde.
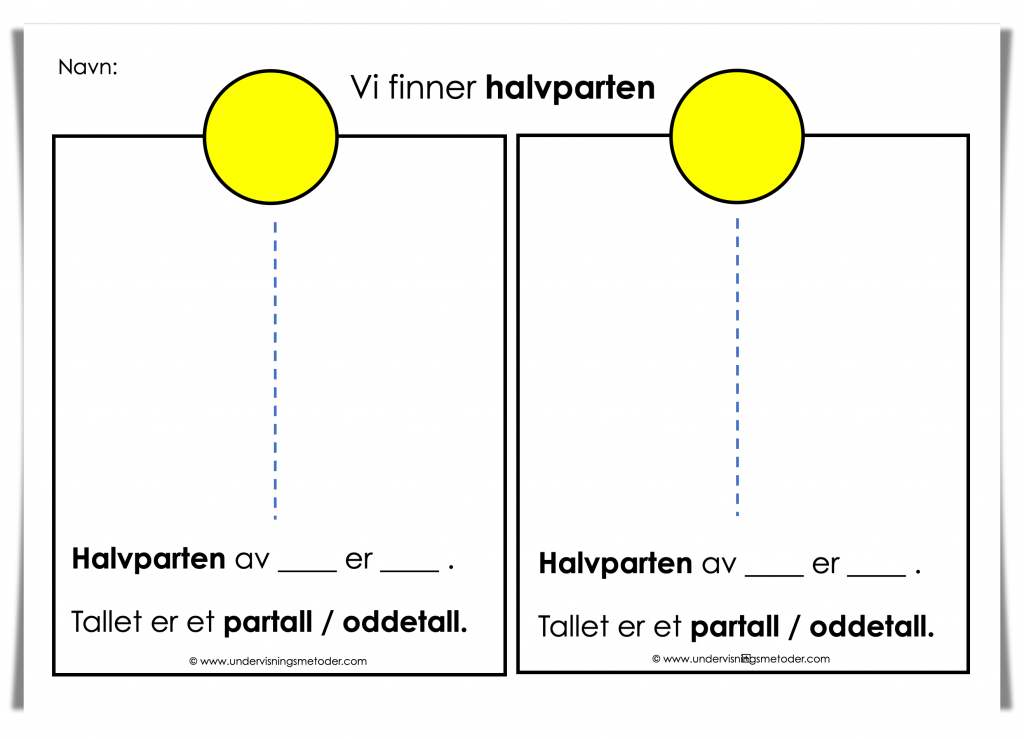
Deretter var oppdraget å lete etter naturmaterialer som kunne brukes til å finne halvparten. Elevene samlet sammen riktig mengde, og fant halvparten ved å fordele like mange på hver side av delestreken. På arbeidsarket fylte elevene inn tallsymbolet, og tegnet for å vise hvordan de fordelte mengden. Deretter fylte de inn nederst på arbeidsarket:
«Halvparten av tallet ___ er ____. Tallet er et partall/oddetall».
Her måtte elevene sette ring rundt begrepet som passet. Deretter løp de tilbake til meg med tallkortet for å få et nytt. Jeg gikk rundt imellom gruppene underveis og sjekket om de hadde forstått oppgaven riktig.

Etter hvert så jeg at stadig flere hadde gjort så mange oppgaver at de hadde forstått prinsippet med hvordan vi finner halvparten. Disse læringspartnerne fikk en ny utfordring; de fikk utdelt et tallkort med oddetall – uten at de visste det!
«Nå skal dere få en ekstra utfordring: For å finne halvparten av dette tallet kan det hende dere må finne en lur måte å tenke på. Jeg sier ikke mer, men er veldig spent på hvordan dere velger å løse oppgaven. LYKKE TIL!»
For noen ivrige elever! De fordelte blader, steiner og pinner på hver side av delestreken, og diskuterte ivrig hva de skulle gjøre med den siste. En gruppe fant ut at de kunne dele bladet på midten i to halve, og legge en halv på hver side. En annen gruppe fant ut at de kunne legge den siste «brikken» midt på delestreken, slik at vi ser at det er en halv på hver side. Dette var en morsom oppdagelse!
Men hvordan skulle elevene klare å skrive en halv? Elevene var hverken kjent med brøk eller å bruke komma. Dette løste de ved å tegne den siste halve. Halvparten av 15 var 7 og en tegning av et halvt blad, noe de leste som «7 og en halv». Og slik oppdaget de at også oddetall kan deles på to, men da må vi dele den siste i to halve.


DEL 3: OPPSUMMERING
Dagen etter startet vi første time med å oppsummere hva vi lærte på uteskolen. Jeg viste bilder fra arbeidet til læringspartnerne, og elevene rakk opp hånda for å fortelle hvordan elevene på bildet hadde tenkt for å løse oppgaven.
Elevene hadde tydeligvis lært, og det gjorde jeg også. Halvparten/dobbelt og oddetall/partall er begreper jeg har undervist i flere ganger, men etter å ha lagt undervisningen ut så jeg hvor mye bedre begrepene satt i forhold til undervisning i samme tema inne i klasserommet. Plutselig kunne elevene finne svaret ved å bruke konkreter, de kunne finne svaret ved å bruke tegning, og ikke minst hadde de forstått innholdet i begrepene. Og dette er læring som sitter. De kan fremdeles finne halvparten av både partall og oddetall, og bruker begrepene aktivt i sitt eget språk. Når vi snakker om halvering, dobling, partall og oddetall i undervisningen husker vi tilbake til hvordan vi jobbet i Sofienbergparken.
Og vipps…
SÅ BLE DET 2 NYE TEMASIDER! 🙂
Både arbeidsarkene og tallkortene som er brukt i dette undervisningsopplegget er lagt ut til gratis nedlastning på to nye temasider: «Tallkort og tallplakater» og «Dobling og halvering». Her finner du mye forskjellig, blant annet uteskoleopplegget med halvering, tallkortene, stafett, regnestrategi-plakater, rebusoppgave og looper til å øve på dobling og halvering. Anbefaler spesielt loopene på det varmeste! De er supre å bruke som utgangspunkt for samarbeidslæring – og ikke minst så er de populære blant elevene.
Kos dere, lær MYE & HA DET KNAKENDE GØY!

